WEB CALCULATRICE
- Conversion monétaire
- Conversion physique
- Constantes physique
- Formules
- Contact
- Nos liens
| Distance à convertir : | |
| Résultat de la conversion: | |
| Superficie à convertir : | |
| Résultat de la conversion : | |
| Volume à convertir : | |
| Résultat de la conversion : | |
| Masse à convertir : | |
| Résultat de la conversion : | |
| Temps à convertir : | |
| Résultat de la conversion : | |
Constantes universelles/Electromagnétisme/Gravitation -
Physico-chimiques -
Atomiques et nucléaires -
Unités de Planck
Célérité
de la lumière dans le vide = 299792458 m·s-1
Perméabilité magnétique du vide = 1,2566370614*10^-6 kg·m·A-2·s-2 (ou H·m-1)
Permittivité diélectrique du vide = 8,854187817*10^-12 A²·s4·kg-1·m-3 (ou F·m-1)
Impédance caractéristique du vide = 376,730313461 kg·m²·A-2·s-3
Constante de Planck = 6,62606957*10^-34 kg·m²·s-1 (ou J·s)
Constante de Planck réduite = 1,054571726*10^-34 kg·m²·s-1
Charge élémentaire = 1,60217662*10^-19 C
Constante de Coulomb = 8,9875517873681764*10^9 kg·m³·A-2·s-4
Constante gravitationnelle = 6,67384*10^-11 m³·kg-1·s-2
Accélération normale de la pesanteur à la surface de la Terre = 9,80665 m·s-2
Perméabilité magnétique du vide = 1,2566370614*10^-6 kg·m·A-2·s-2 (ou H·m-1)
Permittivité diélectrique du vide = 8,854187817*10^-12 A²·s4·kg-1·m-3 (ou F·m-1)
Impédance caractéristique du vide = 376,730313461 kg·m²·A-2·s-3
Constante de Planck = 6,62606957*10^-34 kg·m²·s-1 (ou J·s)
Constante de Planck réduite = 1,054571726*10^-34 kg·m²·s-1
Charge élémentaire = 1,60217662*10^-19 C
Constante de Coulomb = 8,9875517873681764*10^9 kg·m³·A-2·s-4
Constante gravitationnelle = 6,67384*10^-11 m³·kg-1·s-2
Accélération normale de la pesanteur à la surface de la Terre = 9,80665 m·s-2
Température
du point triple de l'eau = 273,16 K
Pression standard de l'atmosphère = 101325 Pa
Nombre d'Avogadro = 6,02214129*10^23 mol-1
Constante des gaz parfaits = 8,3144621 J·K-1·mol-1
Constante de Boltzmann = 1,3806488*10^-23 J·K-1
Constante de Faraday = 96485,3365 C·mol-1
Volume molaire d'un gaz parfait (p = 101,325 kPa, T = 273,15 K) = 22,413968*10^-3 m³·mol-1
Volume molaire d'un gaz parfait (p = 100 kPa, T = 273,15 K) = 22,710953*10^-3 m³·mol-1
Unité de masse atomique = 1,66053886*10^-27 kg
Première constante de rayonnement = 3.74177118*10^-16 W·m²
Première constante de rayonnement pour la radiance spectrale = 1.19104282*10^-16 W·m² sr-1
Deuxième constante de rayonnement = 1.4387752*10^-2 m·K
Constante de Stefan-Boltzmann = 5,670373*10^-8 W·m-2·K-4
Constante de Wien = 2,8977721*10^-3 m·K
Constante de Loschmidt = 2,6867773*10^25 m-3
Pression standard de l'atmosphère = 101325 Pa
Nombre d'Avogadro = 6,02214129*10^23 mol-1
Constante des gaz parfaits = 8,3144621 J·K-1·mol-1
Constante de Boltzmann = 1,3806488*10^-23 J·K-1
Constante de Faraday = 96485,3365 C·mol-1
Volume molaire d'un gaz parfait (p = 101,325 kPa, T = 273,15 K) = 22,413968*10^-3 m³·mol-1
Volume molaire d'un gaz parfait (p = 100 kPa, T = 273,15 K) = 22,710953*10^-3 m³·mol-1
Unité de masse atomique = 1,66053886*10^-27 kg
Première constante de rayonnement = 3.74177118*10^-16 W·m²
Première constante de rayonnement pour la radiance spectrale = 1.19104282*10^-16 W·m² sr-1
Deuxième constante de rayonnement = 1.4387752*10^-2 m·K
Constante de Stefan-Boltzmann = 5,670373*10^-8 W·m-2·K-4
Constante de Wien = 2,8977721*10^-3 m·K
Constante de Loschmidt = 2,6867773*10^25 m-3
Constante
de structure fine = 7,297352568*10^-3
Constante de Rydberg = 1,0973731568525*10^7 m-1
Energie de Hartree = 4,35974417*10^-18 J
Quantum de conductance = 7,748091733*10^-5 S
Quantum de flux magnétique = 2,06783372*10^-15 Wb
Quantum de circulation = 3,636947550*10^-4 m²·s-1
Rayon de Bohr = 5,291772108*10^-11 m
Longueur d'onde de Compton pour l'électron = 2,4263*10^-12 m
Rayon de Compton pour l'électron = 3,861159*10^-13 m
Rayon classique de l'électron = 2,817940325*10^-15 m
Magnéton de Bohr = 9,27400949*10^-24 A·m²
Magnéton nucléaire = 5,05078343*10^-27 A·m²
Masse du proton = 1,67262171*10^-27 kg
Masse du neutron = 1,67492728*10^-27 kg
Masse de l'électron = 9,1093826*10^-31 kg
Masse du muon = 1,88353140*10^-28 kg
Masse du tau = 3,16777*10^-27 kg
Masse du boson Z = 1,62556*10^-25 kg
Masse du boson W = 1,4334*10^-25 kg
Constante de Rydberg = 1,0973731568525*10^7 m-1
Energie de Hartree = 4,35974417*10^-18 J
Quantum de conductance = 7,748091733*10^-5 S
Quantum de flux magnétique = 2,06783372*10^-15 Wb
Quantum de circulation = 3,636947550*10^-4 m²·s-1
Rayon de Bohr = 5,291772108*10^-11 m
Longueur d'onde de Compton pour l'électron = 2,4263*10^-12 m
Rayon de Compton pour l'électron = 3,861159*10^-13 m
Rayon classique de l'électron = 2,817940325*10^-15 m
Magnéton de Bohr = 9,27400949*10^-24 A·m²
Magnéton nucléaire = 5,05078343*10^-27 A·m²
Masse du proton = 1,67262171*10^-27 kg
Masse du neutron = 1,67492728*10^-27 kg
Masse de l'électron = 9,1093826*10^-31 kg
Masse du muon = 1,88353140*10^-28 kg
Masse du tau = 3,16777*10^-27 kg
Masse du boson Z = 1,62556*10^-25 kg
Masse du boson W = 1,4334*10^-25 kg
Constante
de Planck = 6,6260693*10^-34 kg·m²·s-1 (ou J·s)
Constante de Planck réduite = 1,05457168*10^-34 kg·m²·s-1
Masse de Planck = 2,17645*10^-8 kg
Longueur de Planck = 1,61624*10^-35 m
Temps de Planck = 5,39121*10^-44 s
Température de Planck = 1,41679*10^32 K
Charge de Planck = 1,875*10^-18 C
Force de Planck = 1,210*10^44 N
Energie de Planck = 1,956*10^9 J
Puissance de Planck = 3,629*10^52 W
Constante de Planck réduite = 1,05457168*10^-34 kg·m²·s-1
Masse de Planck = 2,17645*10^-8 kg
Longueur de Planck = 1,61624*10^-35 m
Temps de Planck = 5,39121*10^-44 s
Température de Planck = 1,41679*10^32 K
Charge de Planck = 1,875*10^-18 C
Force de Planck = 1,210*10^44 N
Energie de Planck = 1,956*10^9 J
Puissance de Planck = 3,629*10^52 W
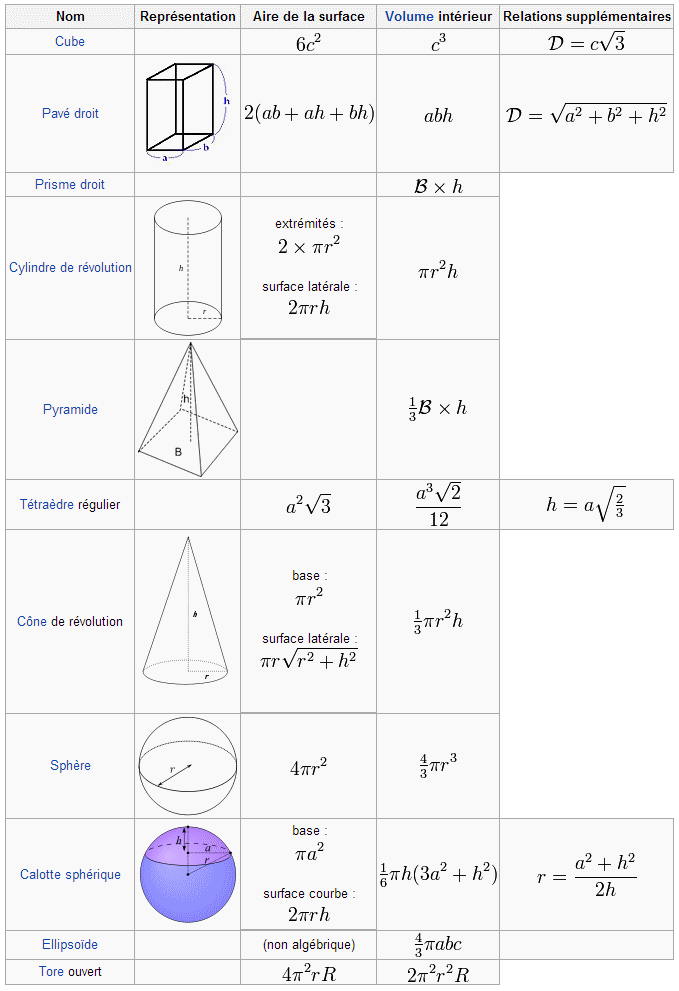
Périmètre et aire - Volume
- Electricité
-
Limites usuelles
- Maths
terminale - Maths
collège -
Energie,thermodynamique -
Développement limité

| I=Q/Δt | I intensité du courant électrique (en ampères) Q la quantité de charges (en coulombs) Δt intervalle de temps (en secondes) |
| U=R*I | U différence de potentiel (en volts) R résistance (en ohms) I intensité (en ampères) |
| ε=Réq*I | ε f.é.m. de la source (en volts) Réq résistance équivalente du circuit (en ohms) I intensité du courant (en ampères) |
| R=(ρ*L)/A | R résistance du composant (en ohms) ρ résistivité du matériau (en ohms-mètres) L longueur du composant (en mètres) A aire de la section du composant (en mètres carrés) |
| Réq=R1+R2+R3+...
1/Réq=1/R1+1/R2+1/R3+... |
pour un circuit en série pour un circuit en parallèle |
| P=U*I | P puissance (en watts) U tension (en volts) I intensité (en ampères) |
| Pmoy=Uéff*Iéff | Equivalent de la formule précédente; s'applique
en courant alternatif Uéff=0,707*Umax Iéff=0,707*Imax |
| P=R*I2 | P puissance dissipée par effet Joule (en watts) R résistance (en ohms) I intensité du courant (en ampères) |
| P=E/(Δt) | P puissance (en watts) E quantité d'énergie (en joules ou en kilowattheures) Δt intervalle de temps (en secondes ou en heures) |
| N1/N2=I2/I1=U1/U2 | N1 et N2 nombres de tours
au primaire et au secondaire d'un transformateur, respectivement U1 et U2 tensions aux bornes du primaire et du secondaire, respectivement (en volts) I1 et I2 intensités du courant dans le primaire et dans le secondaire, respectivement (en ampères) |
| F=(k*|Q1*Q2|)/d2 | F force électrostatique (en newtons) k constante de proportionnalité Q1 et Q2 représentent les charges (en coulombs) d distance (en mètres) |
Limites usuelles de fonctions
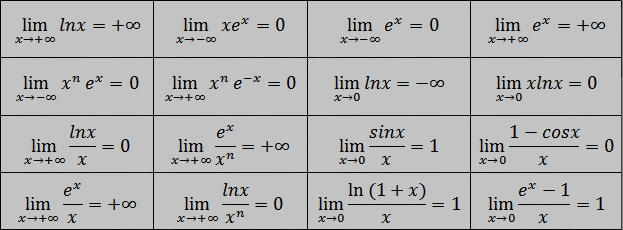
|
Identités remarquables (a+b)²=a²+2ab+b² (a-b)²=a²-2ab+b² (a+b)(a-b)=a²-b² (a+b)³=a³+3a²b+3ab²+b³ (a-b)³=a³-3a²b+3ab²-b³ a³+b³=(a+b)(a²-ab+b²) a³-b³=(a-b)(a²+ab+b²) |
Equation du second degré Soient a, b et c trois nombres réels (a≠0) et Δ=b2 - 4ac. L'équation ax2 + bx + c=0 admet: - Lorsque Δ>0, deux solutions réelles x1=(-b-√Δ)/(2a) x2=(-b+√Δ)/(2a) - Lorsque Δ=0, une solution réelle x1=-b/(2a) - Lorsque Δ<0, aucune solution réelle. Si Δ>0, ax2 + bx + c=a(x-x1)(x-x2) Si Δ=0, ax2 + bx + c=a(x-x1)2 |
||||||||||||||||||||||||||||||||
| Fonctions logarithme et exponentielle e0=1 ea+b=eaeb ea-b=(ea)/(eb) (ea)b=eab lne=1 ln1=0 lnab=lna+lnb lna/lnb=lna-lnb ax=exlna lnax=xlna y=ex⇔x=lny |
Dérivées et primitives
|
Opérations et application des
dérivées (u+v)'=u'+v' (ku)'=ku' (uv)'=u'v+uv' (1/u)'=(-u')/u2 (√u)'=u'/(2√u) (un)'=nu'un-1 (u/v)'=(u'v-uv')/v2 (vºu)'=u'.v'ºu (eu)'=u'eu (lnu)'=u'/u Equation de la tangente à la courbe Cf en A(a; f(a)) : y = f '(a)(x "a)+ f(a) |
|||||||||||||||||||||||||||||||
Trigonométrie
|
|||||||||||||||||||||||||||||||||
Théorème de Pythagore : Si un triangle ABC est rectangle en C
, alors AB2 = AC2 + BC2
Triangle rectangle
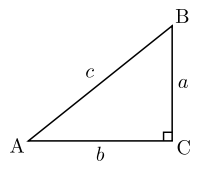 cos(A)=AC/AB
cos(A)=AC/AB
sin(A)=BC/AB
tan(A)=BC/AC
cos(B)=BC/BA
sin(B)=AC/AB
tan(B)=AC/BC
cosinus = côté adjacent / hypoténuse
sinus = côté opposé / hypoténuse
tangente = côté opposé / côté adjacent
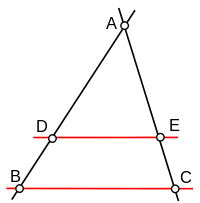
Théorème de Thalès
Soit un triangle ABC, et deux points D et E des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC)
Alors on a : AD/AB = AE/AC et AD/AB = DE/BC
Règle de la distributivité : A X (B + C) = A X B + A X C
Règle de la double-distributivité : (A + B)(C + D) = A X C + A X D + B X C + B X D
Identités remarquables :
(A + B)2 = A2 + B2 + 2AB
(A - B)2 = A2 + B2 - 2AB
(A + B)(A - B) = A2 - B2
Triangle rectangle
 cos(A)=AC/AB
cos(A)=AC/ABsin(A)=BC/AB
tan(A)=BC/AC
cos(B)=BC/BA
sin(B)=AC/AB
tan(B)=AC/BC
cosinus = côté adjacent / hypoténuse
sinus = côté opposé / hypoténuse
tangente = côté opposé / côté adjacent

Théorème de Thalès
Soit un triangle ABC, et deux points D et E des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC)
Alors on a : AD/AB = AE/AC et AD/AB = DE/BC
Règle de la distributivité : A X (B + C) = A X B + A X C
Règle de la double-distributivité : (A + B)(C + D) = A X C + A X D + B X C + B X D
Identités remarquables :
(A + B)2 = A2 + B2 + 2AB
(A - B)2 = A2 + B2 - 2AB
(A + B)(A - B) = A2 - B2
| Travail d'une force | W (J) | W=F.d.cosα |
F : force (N) d : distance sur laquelle elle s'applique (m) α : angle entre le déplacement et la force |
| Puissance d'une force | P (W) | W=F.v.cosα |
F : force (N) v : vitesse à laquelle le point d'application de la force se déplace (m/s) α : angle entre le déplacement et la force |
| Energie cinétique | Ec (J) | Ec=(mv2)/2 |
m : masse du corps (kg) v : vitesse du corps (m/s) |
| Energie potentielle gravitationnelle | Ep (J) | Ep=mgh |
m : masse du corps (kg) g : champ de pesanteur (m/s2 ou N/kg) h : hauteur (m) |
| Puissance | P (W) | P=E/t |
E : énergie (J) t : intervalle de temps (s) |
| Energie au repos | E0 (J) | E0=m0c2 |
m0 : masse au repos (kg) c = 3.108 m/s vitesse de la lumière dans le vide |
Développements limités usuels en 0
sin (x) = x - x3/3! + x5/5! + ... + (-1)p x2p+1/(2p+1)! + o(x2p+1)
cos (x) = 1 - x2/2! + x4/4! + ... + (-1)p x2p/(2p)! + o(x2p)
tan (x) = x + x3/3! + 2x5/15 + o(x6)
sh (x) = x + x3/3! + x5/5! + ... + x2p+1/(2p+1)! + o(x2p+1)
ch (x) = 1 + x2/2! + x4/4! + ... + x2p/(2p)! + o(x2p)
th (x) = x - x3/3! + 2x5/15 + o(x6)
1/(1-x) = 1 + x + ... + xn + o(xn)
1/(1+x) = 1 - x + ... + (-1)n xn + o(xn)
ln (1+x) = x - x2/2 + ... + (-1)n+1 xn/n + o(xn)
ln (1-x) = -x - x2/2 - ... - xn/n + o(xn)
exp (x) = 1 + x + x2/2! + ... + xn/n! + o(xn)
Arctan (x) = x - x3/3 + ... + (-1)n x2n+1/(2n+1) + o(x2n+1)
Vous pouvez envoyer un message à l'équipe de web calculatrice, précisez votre adresse
mail si vous désirez que l'on vous réponde.
Fermer
Fermer
|
|
HISTORIQUE CALCULATRICE
|